19 May 2025
7 minutes read
Ultimate Strategies to Master Arrangements and Combinations GRE for Indian Students

Key Takeaways
- Arrangements and combinations GRE questions demand clear understanding of order and formula application for success.
- Spotting subtle language hints helps Indian students quickly decide between permutations and combinations.
- Pairing solid GRE prep with Ambitio’s profile-building guidance can elevate your GRE quant score and study abroad prospects.
Did you know that arrangements and combinations GRE questions often decide your GRE average score in the quantitative section? Many Indian students struggle because they are confused whether order matters or doesn’t, or forget key permutation and combination formulas under pressure.
You’re not alone, these tricky problems test your grasp of concepts like factorial and the number of permutations. With the right strategies to master these, plus focused GRE prep and practice questions, you can confidently tackle any combination and permutation challenge on test day.
Understanding the Basics of Arrangements and Combinations
When preparing for the GRE quantitative section, mastering the basics of permutation and combination is crucial for effective test prep. At the heart of many permutations problems and combinations problems lies a key question: does the order matter or not?
This determines whether you use a permutation formula or a combination formula to calculate the total number or number of ways to select or arrange objects.
What Are Arrangements (Permutations)?
In permutation questions, the order of selection matters. For example, when 6 people enter a room and are seated around a circular table, many arrangements are possible because changing the sequence creates a new arrangement.
The number of arrangements is calculated using the permutation formula:
P(n,r)= n!/{(n−r)!}
where ‘n’ is the total number of objects, and ‘r’ is the number of selected objects.
What Are Combinations?
On the other hand, in combination or permutation problems where order does not matter, you use combinations. For instance, when choosing a committee of three from 10 members, the focus is on ways of choosing groups without regard to order.
The formula used is:
C(n,r)= n!/{r!(n−r)!}
This calculates the number of ways to select ‘r’ objects from ‘n’ available, useful for GRE quant practice especially in GRE Math convention practice.
Key Differences Between Arrangements and Combinations
| Aspect | Arrangements (Permutations) | Combinations |
|---|---|---|
| Order of selection | Since the order matters | Order does not matter |
| Formula used | P(n,r)=n!/{(n−r)!} | C(n,r)=n!/{r!(n−r)!} |
| Example | Seating 6 people in 6 different chairs | Choosing 3 members from a committee of 10 |
| Number of ways counted | Different sequences count as different arrangements | Groups counted without regard to order |
| Use in GRE Quantitative Section | Common in permutations problems and permutation questions | Common in combinations problems and combination questions |
Important Formulas for Arrangements and Combinations in GRE
Mastering key formulas is essential for acing the GRE test and improving your GRE quantitative score. Understanding permutation formulas and combination formulas helps you tackle complex questions where the test-makers use subtle language to indicate whether you should use a combination or permutation approach.
Permutation Formulas Explained
In permutations problems, the order of selection matters. The most common formula calculates the number of ways to arrange r objects out of n total:
P(n,r)= n!/{(n−r)!}
This helps solve questions involving seating arrangements, like when 6 people enter the room and you want to find many ways can 6 be seated. The multiplication principle applies when you have ‘n’ ways to choose first and ‘m’ ways to choose next.
Combination Formulas Simplified
When a question asks you to choose a group where order does not matter, use combinations:
C(n,r)= n!/{r!(n−r)!}
This is useful for forming groups or sets, such as selecting a committee of three from 10 members. Many test-makers create challenging problems by using subtle language to indicate whether to use permutations or combinations.
Factorials and Their Role in Calculations
The factorial function (n!) is fundamental, representing the total number of ways to arrange n objects without repetition. For example, cards without duplicates or choosing digits for a lock use factorials extensively. Understanding factorials will help you understand quantitative comparison and algebra questions better.
Special Cases in Arrangements and Combinations
Some GRE questions will indicate scenarios like sampling without replacement or seating around a circular table, where formulas slightly differ. For instance, circular arrangements have (n−1)!(n-1)!(n−1)! ways instead of n!n!n!. Recognizing these subtle language to indicate cases can improve your accuracy and speed.
Types of Questions on Arrangements and Combinations in GRE
The GRE quantitative section includes various types of questions on arrangements and combinations GRE that test your understanding of fundamental concepts.
Knowing the difference between permutations and combinations and when to use a combination approach will help you solve problems faster and more accurately.
Simple Arrangement Problems
These questions typically involve finding the number of ways to arrange objects or people in a line or row. For example, 6 ways to seat 6 people or how many ways to arrange one letter words. Such problems require you to calculate number of ways by multiplying the available choices at each step, i.e., 4 ways to choose first, then 3 ways for the next, and so on.
Combination-Based Questions
When the question asks you to choose two or more items where order does not matter, you need to use a combination formula. For instance, selecting cards from a deck of 52 cards or deciding which members to form a committee from many different groups. Test-makers often indicate whether you should use combinations by using subtle language like need to form groups or wants to choose.
Circular Arrangement Questions
Here, objects or people are arranged around a circle, like people seated around a circular table. Unlike linear arrangements, circular ones have fewer number of arrangements due to rotational symmetry. You must consider this to avoid overcounting.
Problems Involving Repetition
Some problems allow repetition, such as forming passwords or choosing digits where an object can be selected multiple times. These require adjusting the basic formulas or using corresponding explanations from your GRE courses to handle such cases correctly.
Mixed Concept Problems
These questions combine concepts, such as first arranging some objects and then choosing others or problems involving sampling without replacement. They often include tricky wording that uses subtle language to indicate which formula or approach to apply. Being able to ace these problems distinguishes top scorers on the GRE test.
By practicing these question types through free GRE study material or structured GRE courses, Indian students can gain the best tips and become able to tackle any permutation or combination question with confidence.
Strategies to Master Permutation and Combinations Questions Quickly
Mastering arrangements and combinations GRE questions is not just about memorizing formulas, it’s about knowing how to quickly identify which approach to use and efficiently solve problems under timed conditions.
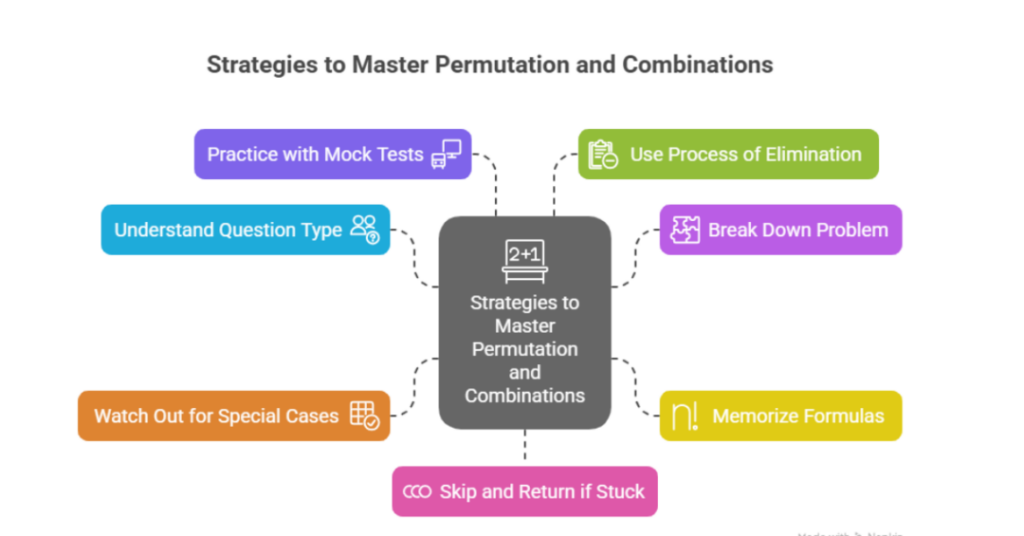
Many Indian students find these questions tricky because of subtle wording and complex scenarios. With focused strategies, you can boost accuracy and speed to confidently ace the GRE quantitative section.
- Understand the Question Type Clearly
Look for keywords that indicate whether you should use permutations or combinations, such as “order matters” or “choose a group.” - Break Down the Problem Step-by-Step
Identify ‘n’ ways and ‘m’ ways parts separately, then apply the multiplication principle to find the total number of arrangements. - Memorize Core Formulas and Factorials
Keep the permutation formula and combination formula handy. Knowing factorials inside out will save crucial time. This will help in GRE time management. - Watch Out for Special Cases
Pay attention to cases like circular arrangements, sampling without replacement, or problems involving repetition. - Practice with Mock Tests and Free GRE Resources
Use resources like Best GRE Online Coaching and proper GRE study plan and practice to get accustomed to the language test-makers use and the problem styles. - Use Process of Elimination in Quantitative Comparison Questions
When stuck, compare quantities to eliminate impossible options quickly. - Skip and Return if Stuck
Don’t spend too much time on a single question. Mark it and move on to maintain good pacing.
By applying these strategies, Indian students can solve arrangements and combinations GRE problems more effectively and maximize their GRE quant practice results.
Practice Problems on Arrangements and Combinations for GRE Math
Practicing a variety of problems is key to mastering arrangements and combinations GRE questions. These 10 problems range from simple to advanced levels, helping Indian students build confidence and improve speed for the GRE quantitative section.
Each question tests important concepts like permutations, combinations, factorials, and special cases. Try solving them on your own before checking the answers!
Simple Level
- Question: How many different ways can 3 letters be arranged from the word “CAT”?
Answer: 3!=6 ways. - Question: From 5 students, how many ways can you choose 2 for a committee?
Answer: (5/2)=5!/(2!⋅3!)=10 ways. - Question: How many ways can 4 people be seated in a row?
Answer: 4!=24 ways. - Question: From a deck of 52 cards, how many ways can you choose 1 card?
Answer: 52 ways. - Question: How many ways to arrange the digits 1, 2, and 3 without repetition?
Answer: 3!=6 ways.
Medium Level
- Question: How many ways can 4 students be seated around a circular table?
Answer: (4−1)!=3!=6 ways. - Question: From 7 books, in how many ways can you choose 3 to take on vacation?
Answer: (7/3)=7!/{3!⋅4!}=35 ways. - Question: How many 3-digit numbers can be formed from digits 1, 2, 3, 4 if digits cannot repeat?
Answer: 4×3×2=24 ways.
Advanced Level
- Question: In how many ways can 5 men and 3 women be seated in a row if all women must sit together?
Answer: Treat the 3 women as one group:
Number of arrangements = (5+1)!×3!=6!×6=720×6=4320 ways - Question: How many different committees of 4 can be formed from 6 men and 5 women if at least 2 women must be on the committee?
Answer:- Committees with 2 women and 2 men: (5/2)×(6/2)=10×15=150
- Committees with 3 women and 1 man: (5/3)×(6/1)=10×6=60
- Committees with 4 women: (5/4)=5
Total = 150+60+5=215 ways.
Conclusion
Understanding arrangements and combinations GRE questions is a vital step for Indian students aiming to excel in the GRE section and boost their overall GRE cut-off. With consistent practice and the right strategies, you can confidently tackle even the toughest permutation and combination problems on test day.
Ready to take your GRE journey to the next level? At Ambitio, we don’t just guide you through test prep, we specialize in building powerful profiles that open doors to top universities abroad.
Join Ambitio Elite today and transform your dream into reality with personalized mentorship, expert insights, and proven success strategies!
FAQs
What’s the difference between permutations and combinations on the GRE?
Permutations involve arranging objects in a specific order, while combinations focus on selecting objects without regard to the order.
How can I improve my GRE quantitative score in permutations and combinations?
Practice regularly, memorize the formulas, and develop a keen eye for recognizing when to use permutations or combinations in GRE math questions.
Are there any free GRE resources for practicing permutations and combinations?
Yes, many online GRE preparation platforms offer free practice questions and explanations to help you master these concepts.
Can you provide an example of a GRE-style permutation and combination question?
Sure, here’s one: “In how many ways can 6 different books be arranged on a shelf?” (Hint: This is a permutation problem.)
What are some common mistakes to avoid when working with permutations and combinations?
Common mistakes include forgetting to use the factorial symbol (!), misinterpreting problem statements, and neglecting to differentiate between permutations and combinations based on problem cues.
How can I tackle complex permutation and combination questions effectively?
Breaking down complex problems into smaller, manageable parts, and applying the appropriate formulas step by step, is an effective strategy. Additionally, practice and familiarity with advanced concepts are crucial.

You can study at top universities worldwide!
Get expert tips and tricks to get into top universities with a free expert session.
Book Your Free 30-Minute Session Now! Book a call now




























