15 Frequently Asked GRE Math Questions With Explanations For Indian Students // Ambitio

Key Takeaways

Frequently asked GRE math questions often mislead students with tricky wording, understanding the question is half the battle.
Strategic thinking and time management matter more than just memorizing formulas for the GRE quant section.
Focused practice with real GRE-style problems and clear explanations helps Indian students improve scores faster.

Did you know over 70% of Indian students struggle with the frequently asked GRE math questions in practice tests, not because they don’t study, but because they don’t recognize how questions trick them? Most practice questions with answers aren’t built to reflect the real GRE quant section.

That’s the harsh truth. But the fix? Learn how to compare the two, find that x, and satisfy the equation, not just solve it. This list unpacks 15 difficult GRE math problems with detailed explanations to help students improve fast.

What to Expect in GRE Math Practice Questions?

Indian students often find the GRE exam deceptively tricky. You’ll face frequently asked GRE math questions like “store sold twice the number” or “ask you to compare,” where the correct answer hides behind clever answer choices. It’s not just about formulas, it’s about logic and time.

Expect types of questions involving area of a triangle, high temperature for x days, or whether quantity B is not always greater. Use free GRE practice questions, sample questions, GRE study materials, and GRE prep course materials to target real exam patterns. To truly improve your GRE score card, practice the 15 hardest GRE math questions with detailed explanations and ace the GRE exam

Expert’s Tips To Answer GRE Math Questions?

The quantitative reasoning section of the GRE is a true test of your problem-solving abilities and mathematical prowess. With a wide range of question types, from data interpretation to quantitative comparison, it’s essential to be prepared with a well-rounded skillset and a calm, focused mindset.

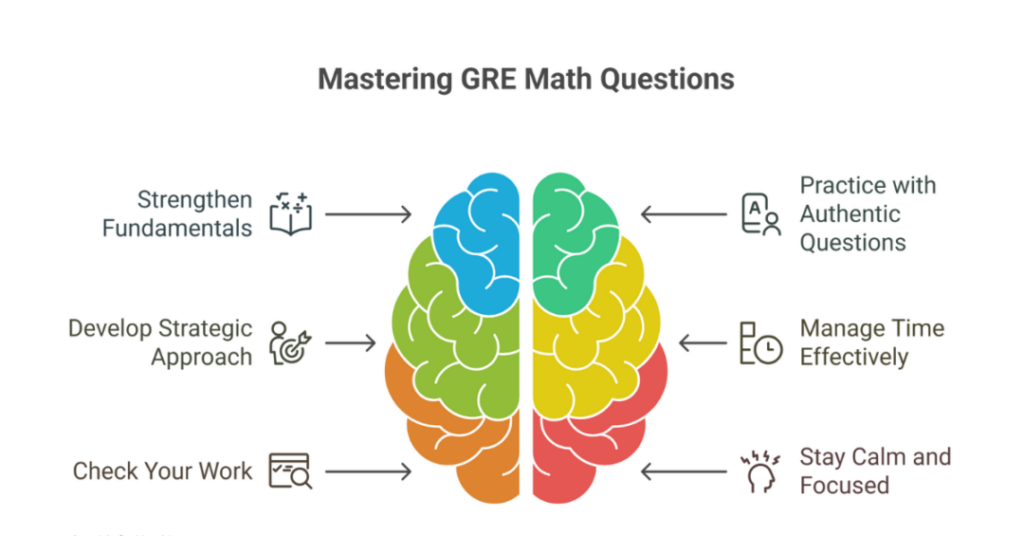
Now, let’s explore some expert GRE quant tips to help you conquer the GRE math questions:

Strengthen Your Fundamentals

Ensure you have a solid grasp of the foundational mathematical concepts covered on the GRE, including arithmetic, algebra, geometry, and data analysis. Revisiting these basics can help you approach questions with confidence and clarity.

Practice with Authentic GRE Questions

Incorporate official GRE practice questions and tests into your preparation routine. These resources will familiarize you with the unique phrasing, format, and difficulty level of the actual GRE questions. It will help you develop the necessary critical thinking and problem-solving skills.

Develop a Strategic Approach

Instead of relying solely on memorization, cultivate a strategic mindset. Learn to identify the core concepts being tested in each question and apply relevant problem-solving techniques, such as plugging in values, working backwards, or visualizing the problem.

Manage Your Time Effectively

Time management skills are crucial in the GRE. Practice pacing yourself and learn to identify questions that may require more time, allowing you to prioritize and allocate your time accordingly during the actual test.

Check Your Work

While working under time pressure, it’s easy to make careless mistakes. Develop a habit of reviewing your work, double-checking GRE calculations, and ensuring your answer aligns with the question being asked.

Stay Calm and Focused

The GRE can be mentally taxing, but maintaining a positive mindset and staying focused is essential. Take breaks when needed, and remember to breathe deeply and stay centred during the test.

5 GRE Multiple-Choice Questions

If you’re an Indian student getting ready for the GRE, you already know the math section isn’t just about calculations, it’s about strategy. Whether you’re solving problems like store sold twice as many or understanding 525 is 10.5%, these frequently asked GRE math questions appear in different disguises. The more you solve, the better you spot patterns, especially when you take a GRE practice test or prepare for graduate schools.

Below are 5 GRE multiple-choice questions with explanations that mirror real exam traps. These are the kinds of questions you’ll likely encounter during the online GRE, so use this as part of your GRE preparation.

1. A store sold 200 units in March. In April, it sold three times the number sold in March. How many were sold in March and April combined?

A. 400
B. 600
C. 800
D. 900
E. 1,000

Correct Answer: B. 800
Explanation:
March = 200 units
April = 3 × 200 = 600 units
Combined = 200 + 600 = 800 units
(This is a classic “store sell in March” problem with ratio traps—watch out.)

2. The sum of the high temperatures for x days is 70 degrees. If an additional day with a high of 80 is added, what is the new average?

A. 70
B. 72
C. 75
D. 80
E. Cannot be determined

Correct Answer: E. Cannot be determined
Explanation:
We only know the sum (not average) is 70, and we don’t know x. Without knowing x, we can’t compute the new average.
(These types of “x days is 70 degrees” questions might look simple but require careful reasoning.)

3. A salesperson earns a salary of $525 plus a commission of 10.5% on all sales. If their total earnings were $1,050, what were their total sales?

A. $5,000
B. $6,000
C. $7,000
D. $7,500
E. $8,000

Correct Answer: D. $7,500
Explanation:
Let x = total sales.
525 + 10.5% of x = 1050 → 525 + 0.105x = 1050
Dividing both sides:
0.105x = 525 → x = $7,500
(Perfect for those working through answered questions on commission and base pay.)

4. If 300 units were sold during those two months, and April combined was 500, how many units were sold in March?

A. 100
B. 200
C. 300
D. 400
E. Cannot be determined

Correct Answer: E. Cannot be determined
Explanation:
The data is inconsistent: if April combined was 500 but sold during those two months is 300, there’s a contradiction.
(These GRE questions might test data sufficiency without saying so.)

5. In a recent dog show, 5 breeds were shown, each with 4 different dogs. If a winner must be selected from each breed, how many combinations are possible?

A. 5
B. 10
C. 20
D. 625
E. 1024

Correct Answer: E. 1024
Explanation:
Each breed: 4 choices
Total combinations: 4^5 = 1024
(These “5 x 4” styled questions are great to test logic under pressure.)

Whether it’s substituting this information into a formula or finding the trap in “quantity B is not always greater,” mastering these problems helps Indian students score higher. Don’t just skim—test with us, try something less obvious, and always look at 15 hard examples to prepare well.

5 GRE Quantitative Comparison Questions

Practicing GRE quantitative comparison questions is invaluable for your preparation. These questions challenge your ability to analyse and compare two quantities, a skill that is essential for success on the quantitative reasoning section.

Here are 5 mostly asked GRE quantitative practice questions:

If x and y are positive integers, is x^2 > y^3

To determine if x^2 > y^3 for positive integers x and y, we need to consider different cases:

If x = 1, then x^2 = 1. For any positive y, y^3 > 1, so x^2 is not greater than y^3.
If y = 1, then y^3 = 1. For any x > 1, x^2 > 1, so x^2 is greater than y^3.
If both x and y are greater than 1, the cube function (y^3) grows faster than the square function (x^2). As x and y increase, y^3 will eventually become greater than x^2.

Therefore, without specific values of x and y, the relationship between x^2 and y^3 cannot be determined for all positive integers x and y. It depends on the values assigned to x and y.

If a and b are integers, is a^2 + b^2 > 2ab?

To determine if a^2 + b^2 > 2ab for integers a and b, we can consider the following cases:

If a = b = 0, then a^2 + b^2 = 0 and 2ab = 0. Therefore, a^2 + b^2 is not greater than 2ab.
If a = 0 and b ≠ 0 (or b = 0 and a ≠ 0), then a^2 + b^2 = b^2 (or a^2) and 2ab = 0. In this case, a^2 + b^2 is greater than 2ab.
If a and b are both non-zero, then a^2 + b^2 > 2ab because (a + b)^2 = a^2 + 2ab + b^2 > a^2 + b^2. This means that a^2 + b^2 is always greater than 2ab when a and b are non-zero integers.

Therefore, for integers a and b, a^2 + b^2 > 2ab is true, except when a = b = 0, in which case a^2 + b^2 = 2ab.

If x and y are positive integers, is x + y > xy?

To determine if x + y > xy for positive integers x and y, we can consider the following cases:

If x = 1 or y = 1, then xy = x or xy = y, respectively. In both cases, x + y is always greater than xy.
If both x and y are greater than 1, we can analyze the inequality by substituting some values:
- For x = 2 and y = 2, we have 2 + 2 = 4 > 2 × 2 = 4
- For x = 3 and y = 3, we have 3 + 3 = 6 > 3 × 3 = 9

In general, for x, y > 1, the product xy will be greater than the sum x + y.

Therefore, for positive integers x and y, the inequality x + y > xy is true only when at least one of x or y is equal to 1. If both x and y are greater than 1, then x + y is not greater than xy.

In summary, x + y > xy is true if x = 1 or y = 1, but false if both x and y are greater than 1.

If a and b are positive integers, is a^2 + b^2 > 2ab?

To determine if a^2 + b^2 > 2ab for positive integers a and b, we can consider the following cases:

If a = b = 1, then a^2 + b^2 = 2 and 2ab = 2. So, a^2 + b^2 is not greater than 2ab.
If either a or b is 1, say a = 1 and b > 1, then a^2 + b^2 = 1 + b^2 and 2ab = 2b. Since b^2 > 2b for b > 1, we have a^2 + b^2 > 2ab.
If both a and b are greater than 1, then (a + b)^2 = a^2 + 2ab + b^2 > a^2 + b^2. This means a^2 + b^2 > 2ab.

Therefore, for positive integers a and b, the inequality a^2 + b^2 > 2ab holds true except when a = b = 1, in which case a^2 + b^2 = 2ab.

If x and y are positive integers, is x^2 + y^2 > 2xy?

To determine if x^2 + y^2 > 2xy for positive integers x and y, we need to consider different cases:

If x = 1 or y = 1, then one of the terms on the left-hand side (x^2 or y^2) becomes 1. In this case, x^2 + y^2 > 2xy always holds true.

For example, if x = 1 and y = 2, we have 1 + 2^2 = 5 > 2(1)(2) = 4.

If both x and y are greater than 1, we can use the algebraic identity (x + y)^2 = x^2 + 2xy + y^2. Rearranging, we get x^2 + y^2 = (x + y)^2 – 2xy > 2xy.

Therefore, for x, y > 1, we have x^2 + y^2 > 2xy.

In summary, the inequality x^2 + y^2 > 2xy holds true for all positive integers x and y, regardless of their values.

The key points are:

If x = 1 or y = 1, the inequality is automatically satisfied.
If x, y > 1, we can use the algebraic identity (x + y)^2 = x^2 + 2xy + y^2 to prove the inequality.

So, for positive integers x and y, x^2 + y^2 is always greater than 2xy.

5 GRE Numeric Entry Questions

Practicing GRE numeric entry questions is invaluable because these questions test your ability to perform precise calculations and provide an exact numerical answer, a skill that is essential in quantitative fields and research-based disciplines.

Here are five examples of GRE numeric entry questions to help you develop this crucial skill:

If x + 3y = 12 and x – y = 4, what is the value of x?

To find the value of x given the equations:

𝑥+3𝑦=12x+3y=12
𝑥−𝑦=4x−y=4

Follow these steps:

Solve the second equation for 𝑥x:

𝑥=𝑦+4x=y+4

Substitute 𝑥x in the first equation:

(𝑦+4)+3𝑦=12(y+4)+3y=12

Simplify and solve for 𝑦y:

𝑦+4+3𝑦=12y+4+3y=12 4𝑦+4=124y+4=12 4𝑦=84y=8 𝑦=2y=2

Substitute 𝑦y back into 𝑥=𝑦+4x=y+4:

𝑥=2+4x=2+4 𝑥=6x=6

So, the value of x is 6.

The sum of three consecutive even integers is 42. What is the smallest of these integers?

Let’s denote the three consecutive even integers as 𝑥x, 𝑥+2x+2, and 𝑥+4x+4.

The sum of these integers is given by:

𝑥+(𝑥+2)+(𝑥+4)=42x+(x+2)+(x+4)=42

Simplify the equation:

𝑥+𝑥+2+𝑥+4=42x+x+2+x+4=42 3𝑥+6=423x+6=42

Subtract 6 from both sides:

3𝑥=363x=36

Divide by 3:

𝑥=12x=12

So, the smallest of these integers is 1212.

A company’s profit is calculated as 25% of its revenue. If the company’s revenue last year was $1,200,000, what was its profit? (Enter your answer as a decimal, rounded to the nearest whole number.)

To calculate the company’s profit, which is 25% of its revenue, follow these steps:

Determine the percentage as a decimal: 25%=0.2525%=0.25
Multiply the revenue by the percentage: Profit=0.25×$1,200,000Profit=0.25×$1,200,000
Perform the multiplication: Profit=$300,000Profit=$300,000

Thus, the company’s profit last year was $300,000.

A rectangular garden has an area of 48 square meters and a length of 8 meters. What is the perimeter of the garden in meters?

To find the perimeter of the rectangular garden, follow these steps:

Calculate the width of the garden using the area and length.

Given: Area=48 square metersArea=48 square meters Length=8 metersLength=8 meters

Width=Area/LengthWidth=Area/Length Width=48/8Width=48/8 Width=6 metersWidth=6 meters

Calculate the perimeter using the formula for the perimeter of a rectangle: Perimeter=2(Length+Width)
Perimeter=2(8+6)
Perimeter=2×14 Perimeter=28 meters
So, the perimeter of the garden is 28 meters.

So, the perimeter of the garden is 28 meters.

If 2x^2 + 3x – 5 = 0, what is the value of x? (Enter your answer as a decimal, rounded to two decimal places.)

To solve the quadratic equation 2𝑥2+3𝑥−5=02×2+3x−5=0, we can use the quadratic formula:

𝑥=−𝑏±𝑏2−4𝑎𝑐2𝑎x=2a−b±b2−4ac

In this equation, 𝑎=2a=2, 𝑏=3b=3, and 𝑐=−5c=−5.

Calculate the discriminant: 𝑏2−4𝑎𝑐=32−4(2)(−5)b2−4ac=32−4(2)(−5) =9+40=9+40 =49=49
Substitute the values into the quadratic formula: 𝑥=−3±492×2x=2×2−3±49 𝑥=−3±74x=4−3±7

This gives us two possible solutions:

Calculate the first solution: 𝑥=−3+74x=4−3+7 𝑥=44x=44 𝑥=1x=1
Calculate the second solution: 𝑥=−3−74x=4−3−7 𝑥=−104x=4−10 𝑥=−2.5x=−2.5

So, the solutions are 𝑥=1x=1 and 𝑥=−2.5x=−2.5.

The values of 𝑥x rounded to two decimal places are: 𝑥=1.00 and 𝑥=−2.50x=1.00 and x=−2.50

Conclusion

Preparing for the GRE math section doesn’t have to be overwhelming. By focusing on the most frequently asked questions and employing strategic problem-solving techniques, you can boost your confidence and your score. Remember, consistent practice and a solid understanding of fundamental concepts are key to success.

As you practice, take time to reflect on your mistakes. Understanding why you got a question wrong is just as important as knowing the right answer. This reflection helps you identify patterns in your thinking and strengthens your problem-solving skills, ensuring you’re better prepared for test day.

Navigate your path to GRE success with Ambitio’s precision preparation. Designed for ambitious students, our platform provides a strategic approach to the GRE, offering in-depth content review, practice tests, and personalized feedback to optimize your study time and results.

FAQs

What types of math questions are on the GRE?

The GRE Quantitative Reasoning section tests your knowledge of arithmetic, algebra, geometry, and data analysis . This includes topics like properties of integers, arithmetic operations, exponents, equations, coordinate geometry, probability, and statistics.

How many math questions are on the GRE?

The GRE has two 35-minute Quantitative Reasoning sections, each with 20 questions, for a total of 40 math questions. The questions are a mix of multiple choice, quantitative comparison, and numeric entry formats.

What is the best way to practice GRE math?

The key to improving your GRE math skills is to practice a wide variety of questions, identify your weaknesses, and learn from your mistakes. Work through practice questions, review explanations for questions you got wrong, and focus on the areas you struggle with the most.

Are there any shortcuts or tricks for GRE math?

While there are some useful strategies like plugging in numbers or using the process of elimination, the best approach is to master the underlying math concepts. Shortcuts can be risky if you don’t fully understand the reasoning behind them.

How hard are the math questions on the GRE?

The difficulty of GRE math questions varies, with some being relatively straightforward and others being quite challenging . The second Quant section will be harder if you perform well on the first section. Practicing a mix of easy, medium, and hard questions is ideal.

What is the best way to study for the GRE math section?

Effective GRE math prep involves taking practice tests, reviewing explanations, and focusing on your weakest areas . Use a variety of resources like practice questions, flashcards, videos, and books. Studying with a tutor or in a class can also be very helpful for many students.